Examples
-
//Definitions that are Black-Box equivalent
#include <iostream>
using namespace std;
double new_balance(double balance_par, double rate_par);
//Returns the balance in a bank account after
//posting simple interest. The formal parameter balance_par is
//the old balance. The formal parameter rate_par is the interest rate.
//For example, if rate_par is 5.0, then the interest rate is 5%
//and so new_balance(100, 5.0) returns 105.00.
int main( )
{
double balance = 100;
cout.setf(ios::fixed);
cout.setf(ios::showpoint);
cout.precision(2);
cout << "balance = $" << balance << endl;
cout << "new balance = $" << new_balance(balance, 5.5) << endl;
cout << "Now edit the program comment so the other definition is used.\n";
return 0;
}
//Definition 1
double new_balance(double balance_par, double rate_par)
{
double interest_fraction, interest;
interest_fraction = rate_par/100;
interest = interest_fraction*balance_par;
return (balance_par + interest);
}
/*Definition 2
double new_balance(double balance_par, double rate_par)
{
double interest_fraction, updated_balance;
interest_fraction = rate_par/100;
updated_balance = balance_par*(1 + interest_fraction);
return updated_balance;
}*/
-
//Computes the average yield on an experimental pea growing patch.
#include <iostream>
using namespace std;
double est_total(int min_peas, int max_peas, int pod_count);
//Returns an estimate of the total number of peas harvested.
//The formal parameter pod_count is the number of pods.
//The formal parameters min_peas and max_peas are the minimum
//and maximum number of peas in a pod.
int main( )
{
int max_count, min_count, pod_count;
double average_pea, yield;
cout << "Enter minimum and maximum number of peas in a pod: ";
cin >> min_count >> max_count;
cout << "Enter the number of pods: ";
cin >> pod_count;
cout << "Enter the weight of an average pea (in ounces): ";
cin >> average_pea;
yield =
est_total(min_count, max_count, pod_count) * average_pea;
cout.setf(ios::fixed);
cout.setf(ios::showpoint);
cout.precision(3);
cout << "Min number of peas per pod = " << min_count << endl
<< "Max number of peas per pod = " << max_count << endl
<< "Pod count = " << pod_count << endl
<< "Average pea weight = " << average_pea << " ounces" << endl
<< "Estimated average yield = " << yield << " ounces" << endl;
return 0;
}
double est_total(int min_peas, int max_peas, int pod_count)
{
double average_pea;
average_pea = (max_peas + min_peas)/2.0;
return (pod_count * average_pea);
}
-
//Computes the area of a circle and the volume of a sphere.
//Uses the same radius for both calculations.
#include <iostream>
#include <cmath>
using namespace std;
const double PI = 3.14159625358979; // global constants.
// No global variables are allowed in this course!!!
double area(double radius);
//Returns the area of a circle with the specified radius.
double volume(double radius);
//Returns the volume of a sphere with the specified radius.
void show_results(double radius, double area, double volume);
int main( )
{
double radius_of_both, area_of_circle, volume_of_sphere;
cout << "Enter the radius: ";
cin >> radius_of_both;
area_of_circle = area(radius_of_both);
volume_of_sphere = volume(radius_of_both);
show_results(radius_of_both,
area_of_circle, volume_of_sphere);
return 0;
}
double area(double radius)
{
return (PI * pow(radius, 2));
}
double volume(double radius)
{
return ((4.0/3.0) * PI * pow(radius, 3));
}
//Uses iostream:
void show_results(double radius, double area, double volume)
{
cout << "Radius = " << radius << " inches\n"
<< "Area of circle = " << area
<< " square inches\n"
<< "Volume of sphere = " << volume
<< " cubic inches\n";
}
-
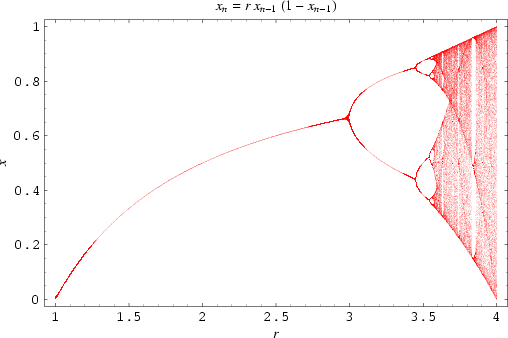
// Programming the logistic map to demonstrate how a simple system
// can go from well-behaved to chaotic behavior.
// The logistic map is a simple iterative map:
// x(n) = a x(n-1) [1 - x(n-1)] n = 1, 2, ...,
// starting from an initial value x(0).
// Besides x(0), a is another parameter in the problem.
// For a in [0, 1], x always goes to 0 asymptotically.
// For a in [1, 3], x asymptotically approach an a-dependent value.
// For a in [3, 3.44949...], x asymptotically jumps alternately between 2 values.
// This is called period doubling.
// For a larger than 3.569945672, the system enters into the chaotic regime where
// a slight change in the initial value for x will lead to drastically
// different temporal behavior
#include <iostream>
using namespace std;
void HWassignment(int HW_number, int month, int day, int year);
double logistic_map(double a, double x);
int main( )
{
// There is really no need to iterate the map so many steps
// All I want to show you is that the program runs so quickly on
// today's computer that even going through the loop 20 million times,
// it takes only a second or so.
const int MAX_COUNT =2000;
int count = 0;
double parameter, x;
HWassignment(24,10,1,2003);
cout << "Enter the logistic map parameter: ";
cin >> parameter;
cout << "Enter an initial value for x: ";
cin >> x;
while (count < MAX_COUNT)
{
// If you run the iteration over a million times then you should
// comment out the following line to suppress output to the screen
// until the end of the loop, otherwise it would really slow down the
// program since screen output is EXTREMELY slow compared to the CPU.
cout << "x = " << x << endl;
x = logistic_map(parameter,x);
count++;
}
cout << "x = " << x << endl;
return 0;
}
void HWassignment(int HW_number, int month, int day, int year)
{
cout << "Name: AL Einstein\n";
cout << "ID: 299792458\n";
cout << "HW: " << HW_number << endl;
cout << "Date: " << month << '/' << day << '/' << year << endl << endl;
}
double logistic_map(double a, double xx)
{
xx = a * xx * (1.0 - xx);
return xx;
}