VIBRATION MODES OF A LINEAR TRIATOMIC MOLECULE
Required mathematical background: Matrix eigenvalues and eigenfunctions.
A study of the vibration modes of a linear triatomic molecule is used to
illucidate the meaning of eigenvalues and eigenvectors in linear algebra.
Let 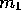 ,
, 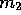 and
and 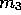 be the masses of the atoms of a triatomic molecule.
For simplicity, the motions of the atoms are constrained to lie along the x-axis.
Their equilibrium positions are labeled by
be the masses of the atoms of a triatomic molecule.
For simplicity, the motions of the atoms are constrained to lie along the x-axis.
Their equilibrium positions are labeled by 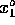 ,
, 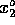 and
and 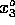 .
At time t, the positions of the atoms as measured from their respective
equilibrium positions are
.
At time t, the positions of the atoms as measured from their respective
equilibrium positions are
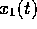 ,
, 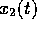 and
and  .
.
Assuming that the deviations of the atoms from their equilibrium positions
are small compared with the interatomic separations, the potential energy
function has the following form:
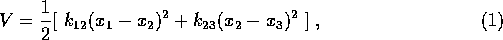
where 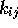 is the spring constant connecting atom i and
atom j.
is the spring constant connecting atom i and
atom j.
The kinetic energy is
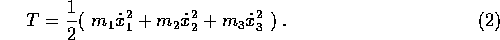
Newton's equations of motion
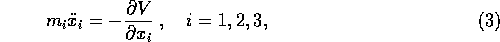
give
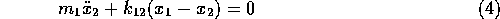

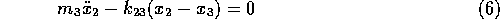
To further simplify the algebra, it is assumed that atoms 1 and 3 are
identical and so 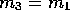 and
and 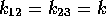 .
For example, the system may represent a
.
For example, the system may represent a 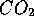 molecule.
It is clear that the time dependence of the displacements must have the form
molecule.
It is clear that the time dependence of the displacements must have the form
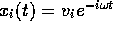 , and so the following matrix eigenvalue
problem is obtained:
, and so the following matrix eigenvalue
problem is obtained:

where
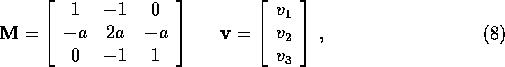
with  and
and
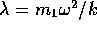 .
The eigenvalue
.
The eigenvalue 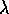 gives a measure of the square of the vibration
frequency.
Matrix
gives a measure of the square of the vibration
frequency.
Matrix 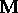 is
is 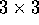 because there are three atoms moving along a single direction. Therefore there are 3 eigenvalues which give three normal
mode vibration frequencies. These eigenvalues are obtained from the equation
because there are three atoms moving along a single direction. Therefore there are 3 eigenvalues which give three normal
mode vibration frequencies. These eigenvalues are obtained from the equation

where 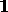 is the
is the
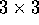 identity matrix.
identity matrix.
Expanding the determinant along the first column, for example,
yields the equation
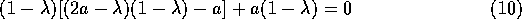
which can be factored to give
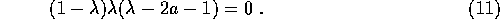
The eigenvalues are 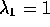 ,
, 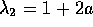 and
and
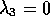 .
The corresponding un-normalized eigenvectors can easily be found and they are
.
The corresponding un-normalized eigenvectors can easily be found and they are
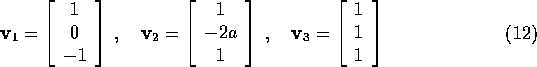
From the eigenvector 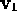 it is clear that the first mode corresponds
to a vibrational pattern in which the atom in the middle is stationary while
the atoms at the ends vibrate with the same amplitude but
it is clear that the first mode corresponds
to a vibrational pattern in which the atom in the middle is stationary while
the atoms at the ends vibrate with the same amplitude but
 out of phase with each other.
out of phase with each other.
The second mode corresponds to a situation in which the two atoms at the ends
vibrate in phase with each other but 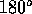 out of phase with the atom in the
middle. Also the amplitude of vibration is larger for the middle atom than that
of the end atoms.
out of phase with the atom in the
middle. Also the amplitude of vibration is larger for the middle atom than that
of the end atoms.
Frequency of vibration of the third mode is zero and so it is clearly not a
vibration at all. From the corresponding eigenvector, 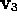 ,
it is obvious that this mode corresponds to a rigid translation of the entire
molecule. This mode exists because there is no net force exerted on the
center-of-mass of the molecule as a whole.
,
it is obvious that this mode corresponds to a rigid translation of the entire
molecule. This mode exists because there is no net force exerted on the
center-of-mass of the molecule as a whole.
A more vivid picture of the first and second mode can be obtained by exploring
the
Java applet which shows an animation of these modes.
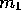 ,
, 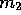 and
and 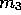 be the masses of the atoms of a triatomic molecule.
For simplicity, the motions of the atoms are constrained to lie along the x-axis.
Their equilibrium positions are labeled by
be the masses of the atoms of a triatomic molecule.
For simplicity, the motions of the atoms are constrained to lie along the x-axis.
Their equilibrium positions are labeled by 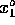 ,
, 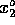 and
and 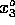 .
At time t, the positions of the atoms as measured from their respective
equilibrium positions are
.
At time t, the positions of the atoms as measured from their respective
equilibrium positions are
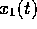 ,
, 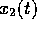 and
and  .
.
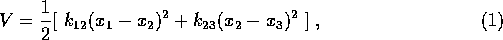
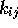 is the spring constant connecting atom i and
atom j.
is the spring constant connecting atom i and
atom j.
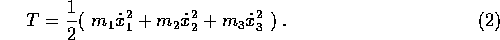
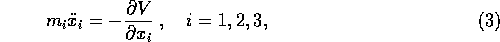
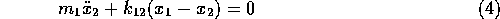

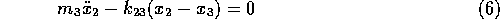
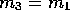 and
and 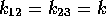 .
For example, the system may represent a
.
For example, the system may represent a 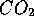 molecule.
It is clear that the time dependence of the displacements must have the form
molecule.
It is clear that the time dependence of the displacements must have the form
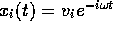 , and so the following matrix eigenvalue
problem is obtained:
, and so the following matrix eigenvalue
problem is obtained:

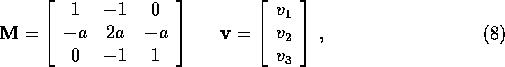
 and
and
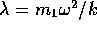 .
The eigenvalue
.
The eigenvalue 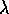 gives a measure of the square of the vibration
frequency.
Matrix
gives a measure of the square of the vibration
frequency.
Matrix 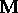 is
is 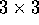 because there are three atoms moving along a single direction. Therefore there are 3 eigenvalues which give three normal
mode vibration frequencies. These eigenvalues are obtained from the equation
because there are three atoms moving along a single direction. Therefore there are 3 eigenvalues which give three normal
mode vibration frequencies. These eigenvalues are obtained from the equation

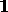 is the
is the
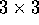 identity matrix.
identity matrix.
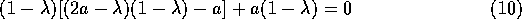
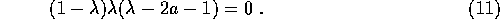
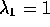 ,
, 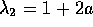 and
and
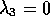 .
The corresponding un-normalized eigenvectors can easily be found and they are
.
The corresponding un-normalized eigenvectors can easily be found and they are
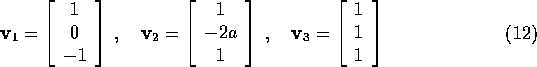
 it is clear that the first mode corresponds
to a vibrational pattern in which the atom in the middle is stationary while
the atoms at the ends vibrate with the same amplitude but
it is clear that the first mode corresponds
to a vibrational pattern in which the atom in the middle is stationary while
the atoms at the ends vibrate with the same amplitude but
 out of phase with each other.
out of phase with each other.
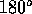 out of phase with the atom in the
middle. Also the amplitude of vibration is larger for the middle atom than that
of the end atoms.
out of phase with the atom in the
middle. Also the amplitude of vibration is larger for the middle atom than that
of the end atoms.
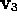 ,
it is obvious that this mode corresponds to a rigid translation of the entire
molecule. This mode exists because there is no net force exerted on the
center-of-mass of the molecule as a whole.
,
it is obvious that this mode corresponds to a rigid translation of the entire
molecule. This mode exists because there is no net force exerted on the
center-of-mass of the molecule as a whole.